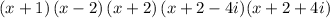Question

F(x) = X5 + 5x4 + 20x3 - 96x - 80 Has Some Of Its Zeros As X = -2, -1,2 What Would Be The Factorization Of F(x)? A. (x + 2)(x + 1)(x-2

Answer 1

`\left(x+1\right)\left(x-2\right)\left(x+2\right)(x +2 - 4i)(x +2 + 4i)`

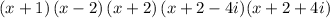
Explanation:

Given

`f(x) = x^5 + 5x^4 + 20x^3 - 96x - 80`

`Zeros: -2, -1, 2`

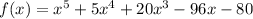
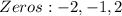
Required

Factorization of f(x)

The given zeros imply that:

`x=-2`
`x =-1`
`x = 2`

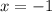
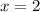
This gives:

`x + 2 =0`
`x + 1 = 0`
`x - 2 = 0`

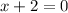
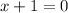
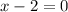
So, some factors are:

(x + 2), (x + 1) and (x - 2)

Divide f(x) by the factors, to get the other factors:

`(x^5 + 5x^4 + 20x^3 - 96x - 80)/((x + 2)(x + 1) (x - 2))`

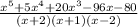
Using a factorization calculator, we have:

`(\left(x+1\right)\left(x-2\right)\left(x+2\right)\left(x^2+4x+20\right))/((x + 2)(x + 1) (x - 2))`

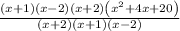
Cancel out common terms

`x^2+4x+20`

Using quadratic formula, we have:

`x = (-b \± √(b^2 - 4ac))/(2a)`

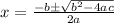
Where

`a = 1; b =4; c = 20`

`x = (-4 \± √(4^2 - 4*1*20))/(2*1)`

`x = (-4 \± √(16 - 80))/(2*1)`

`x = (-4 \± √(-64))/(2)`

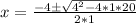
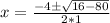
Using complex notation

`√(-64)= 8i`

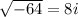
So:

`x = (-4 \± 8i)/(2)`

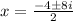
Simplify the fraction

`x = -2 \± 4i`

Split

`x = -2 + 4i \ or\ x = -2 - 4i`

Equate to 0

`x +2 - 4i = 0 \ or\ x +2 + 4i = 0`

The other factors are: (x +2 - 4i) and (x +2 + 4i)

Hence, the factorization of f(x) is:

`\left(x+1\right)\left(x-2\right)\left(x+2\right)(x +2 - 4i)(x +2 + 4i)`