Question

What is the equation of the line that is the parallel to x - 8y = 16 and passes throguh the point (-8, 2)

Answer 1

`\displaystyle x - 8y = -24\:or\:y = (1)/(8)x + 3`

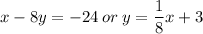
Step-by-step explanation:

First off, convert this standard equation to a Slope-Intercept equation:

`\displaystyle x - 8y = 16 \hookrightarrow (-8y)/(-8) = (-x + 16)/(-8) \\ \\ \boxed{y = (1)/(8)x - 2}`

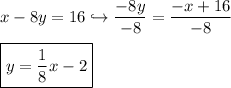
Remember, parallel equations have SIMILAR RATE OF CHANGES, so ⅛ remains as is as you move forward with plugging the information into the Slope-Intercept Formula:

`\displaystyle 2 = (1)/(8)[-8] + b \hookrightarrow 2 = -1 + b; 3 = b \\ \\ \boxed{\boxed{y = (1)/(8)x + 3}}`

Now, suppose you need to write this parallel equation in Standard Form. You would follow the procedures below:

y = ⅛x + 3

- ⅛x - ⅛x

__________

−⅛x + y = 3 [We CANNOT leave the equation this way, so multiply by –8 to eradicate the fraction.]

−8[−⅛x + y = 3]

`\displaystyle x - 8y = -24`

With that, you have your equation(s).

`\displaystyle -x + 8y = 24`

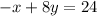
*About this equation, INSTEAD of multiplying by –8, you multiply by its oppocite, 8. Now, you can leave it like this, but UNIVERSALLY, the A-term is positive, so you must multiply the negative out as well.

I am joyous to assist you at any time.

Answer 2

Explanation:

x - 8y = 16

Write in slope-intercept form: y = mx + b

-8y = -x + 16

Divide the entire equation by (-8)

`y =(-1)/(-8)x+(16)/(-8)\\\\\\y=(1)/(8)x-2`

Parallel lines have slope. So, the slope of the required line = 1/8

`y =(1)/(8)x+b\\\\\\`

(-8,2) is on the line. so, plugin the values in the above equation and find the y-intercept b

`2=(1)/(8)*(-8)+b\\\\\\2=-1+b\\\\b = 2+1\\\\b = 3\\\\Equation \ of \ the \ required \ line:\\\\y=(1)/(8)x+3`