Question

The exponential decay function A = A0(1/2)^t/P can be used to determine the amount A, of a radioactive substance present at time t, if A0 represents the initial amount and P represents the half-life of the substance.

If a substance loses 70% of its radioactivity in 500 days, determine the period of the half-life.
Show your work.

Answer 1

The half-life of the substance is about 288 days.

Explanation:

The exponential decay function:

`\displaystyle A=A_0\left((1)/(2)\right)^(t/P)`

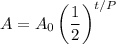
Can determine the amount A of a radioactive substance present at time t. A₀ represents the initial amount and P is the half-life of the substance.

We are given that a substance loses 70% of its radioactivity in 500 days, and we want to determine the period of the half-life.

In other words, we want to determine P.

Since the substance has lost 70% of its radioactivity, it will have only 30% of its original amount. This occured in 500 days. Therefore, A = 0.3A₀ when t = 500 (days). Substitute:

`\displaystyle 0.3A_0=A_0\left((1)/(2)\right)^(500/P)`

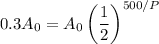
Divide both sides by A₀:

`\displaystyle 0.3=\left((1)/(2)\right)^(500/P)`

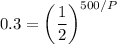
We can take the natural log of both sides:

`\displaystyle \ln(0.3)=\ln\left(\left((1)/(2)\right)^(500/P)\right)`

Using logarithmic properties:

`\displaystyle \ln(0.3)=(500)/(P)\left(\ln\left((1)/(2)\right)\right)`

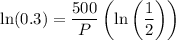
So:

`\displaystyle (500)/(P)=(\ln(0.3))/(\ln(0.5))`

Take the reciprocal of both sides:

`\displaystyle (P)/(500)=\displaystyle (\ln(0.5))/(\ln(0.3))`

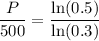
Use a calculator:

`\displaystyle P=(500\ln(0.5))/(\ln(0.3))\approx287.86`

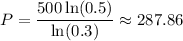
The half-life of the substance is about 288 days.