Answer:
The expected number of keys she will try before she opens the door is 4.5.
Explanation:
Probability of opening with the first key:
One key out of 8 working, so: 1/8 probability of opening with the first key, that is:

Probability of opening with the second key:
Doesn't work on the first(7/8 probability), works on the second(1/7 probability). So
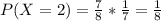
Following the logic:
For each value of x from 1 to 8, we have that
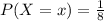
Find the expected number of keys she will try before she opens the door.
Each outcome multiplied by its probability. So

The expected number of keys she will try before she opens the door is 4.5.