Answer:
0.33 moles of aluminum are necessary to produce 11 L of hydrogen gas at STP.
Step-by-step explanation:
The STP conditions refer to the standard temperature and pressure. Pressure values at 1 atmosphere and temperature at 0 ° C are used and are reference values for gases. And in these conditions 1 mole of any gas occupies an approximate volume of 22.4 liters.
You can apply the following rule of three: if by STP conditions, 22.4 L represents 1 mole of hydrogen, 11 L how many moles will they be?
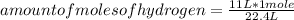
amount of moles of hydrogen= 0.491 moles
On the other side, the balanced reaction is:
2 AI + 6 HCI → 2 AICI₃ + 3 H₂
By reaction stoichiometry, the following amounts of moles of each compound participate in the reaction:
- AI: 2 moles
- HCI: 6 moles
- AICI₃: 2 moles
- H₂: 3 moles
Then you can apply the following rule of three: if 3 moles of hydrogen are produced by 2 moles of aluminum, 0.491 moles of hydrogen are produced by how many moles of aluminum?

amount of moles of aluminum= 0.33 moles
0.33 moles of aluminum are necessary to produce 11 L of hydrogen gas at STP.