Answer:
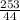
Explanation:
ignore the "at the instant the man is 30 feet away" part, set it as X and the man's shadow as Y.
Similar triangles so we can do
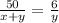 .
.
Solve for it we get 44y = 6x
Differentiate relative to time t, we get 44y' = 6x'.
change in x (x') is equal to 5. And we get the answer y' =
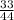 .
.
the
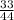 ft/sec is the rate of which the length of the shadow is changing. add 5 to it for the rate of the tip of his shadow moving away from the tower.
ft/sec is the rate of which the length of the shadow is changing. add 5 to it for the rate of the tip of his shadow moving away from the tower.