Question

Please help me Please this is due today

Show that p(x) is divisible by q(x) in each of the
following cases.
​

Answer 1

See Below.

Explanation:

By the Factor Theorem, if we divide q(x) into p(x) and the resulting remainder is 0, then p(x) is divisible by q(x) (i.e. there are no remainders).

Problem 1)

We are given:

`p(x)=x^3+3x^2+3x+1\text{ and } q(x)=x+1`

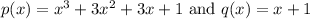
We should find the remainder when dividing p(x) and q(x). We can use the Polynomial Remainder Theorem. When dividing a polynomial p(x) by a binomial in the form of (x - a), then the remainder will be p(a).

Here, our divisor is (x + 1) or (x - (-1)). So, a = -1.

Then by the Polynomial Remainder Theorem, the remainder when performing p(x)/q(x) is:

`p(-1)=(-1)^3+3(-1)^2+3(-1)+1=0`

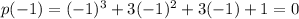
The remainder is 0, satisfying the Factor Theorem. p(x) is indeed divisible by q(x).

Problem 2)

We are given:

`p(x)=x^3-2x^2+6x-27\text{ and } q(x)=x-3`

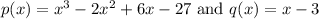
Again, use the PRT. In this case, a = 3. So:

`p(3)=(3)^3-2(3)^2+6(3)-27=0`

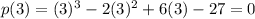
It satisfies the Factor Theorem.

Problem 3)

We are given:

`p(x)=x^n-10^n\text{ and } q(x)=x-10`

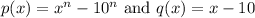
Use the PRT. In this case, a = 10. So:

`p(10)=(10)^n-10^n=0`

It satisfies the Factor Theorem.

Since all three cases satisfy the Factor Theorem, p(x) is divisible by q(x) in all three instances.