Question

For the function given below, find a formula for the Riemann sum obtained by dividing the interval [1,4] into n equal subintervals and using the right-hand endpoint for each ck. Then take a limit of this sum as n -> infinite to calculate the area under the curve over [1: 4].

f(x) = 4x

Answer 1

`\sum \limits ^(n)_(k=1) 4 \Big [ 1 + (3k)/(n) \Big] \Big [ (3)/(n) \Big ]`

Explanation:

Given the function:

f(x) = 4x; we are to determine the expression given the Reimman sum formula for the given function f(x) = 4x over the interval [1,4]

Since;

`\Delta x = (4-1)/(x) = (3)/(x) \\ \\ x_i = a+ \Delta x_i`

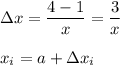
where;

a = 1 and Δ = 4

∴

`x_i = 1+ (3)/(x)i`

For i = k

`x_k = 1+ (3)/(x)k`

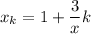
However;

`y(x_i) = 4x \\ \\ y(x_i) = 4(1 +(3i)/(x))`

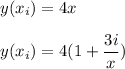
Thus, the formula for the Reinmann sum is:

`\sum \limits ^(n)_(k=1) \Big [ 4 \Big [ 1 + (3i)/(x) \Big] \Big ] \Delta x \\ \\ \\ \sum \limits ^(n)_(k=1) \Big [ 4 \Big [ 1 + (3k)/(x) \Big] \Big ] (3)/(x)`

Since we are taking the limit as n → ∞

`\sum \limits ^(n)_(k=1) 4 \Big [ 1 + (3k)/(n) \Big] \Big [ (3)/(n) \Big ]`