Question

Explain how you can find the side length of a rectangular prism if you are given the volume and the 2 other measurements. Does this process change if one of the measurements is a fraction?

Answer 1

The volume of a rectangular prism can be calculated by the formula:

• Volume of a rectangular prism = length * width * height

If the exercise give us the volume and the two other measurements (width and height), we must simplify the length from the formula showed (remember when a value is multiplying in a side to the equal sign, go to the other side to divide):

• (Volume of a rectangular prism) / (width * height) = length

Or, in other form:

• 
  `length=(volume)/(width*height)`

At last, the proccess change only a little if one is a fraction, in that case, you should just multiply or divide with that fraction.

Explanation:

We're gonna take measurements for the volume, width and height to solve a hypothetical exercise:

• Volume = 240
  `in^(3)`
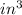
• Width = 4 in
• Height = 12 in

We use the formula in the answer:

• 
  `length=(volume)/(width*height)`

Replacing the data we obtain:

• 
  `length=(240in^(3) )/(4 in *12in )`
• 
  `length=(240in^(3) )/(48in^(2) )`
• 
  `length=` 5 inches

Now, we're gonna make the a hypothetical exercise where a measurement is a fraction, we can select anyone, in this case will be the width:

• Volume = 48
  `in^(3)`
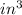
• Width = 8/3 in
• Height = 6 in

We use the same formula and replace again:

`length=(volume)/(width*height)`

• 
  `length=(48in^(3) )/((8)/(3)in *6 in)`
• 
  `length=(48in^(3) )/(16in^(2) )`
• 
  `length=` 3 inches

As you can see, the process does't change much using fractions, you must only know the correct form to operate these.