Question

¿Para cuál(es) valor(es) de p las rectas de ecuación x − 1/p = 2 − y/p y x − 1/1 − p = y − 2/2 son perpendiculares? A) Solo para el 3 B) Solo para el 1 C) Solo para el -1 D) Solo para el -3 E) Para el 0 y el -1

Answer 1

Respuesta:

C) Solo para el -1

Explicación paso a paso:

Para resolver este problema, debemos de determinar la pendiente en cada una de las ecuaciones provistas:

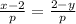
`(x-2)/(p)=(2-y)/(p)`

y

`(x-1)/(1-p)=(y-2)/(2)`

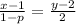
ahora bien, necesitamos conocer el valor de la pendiente de una de las dos ecuaciones. Tomemos la primera ecuación y resolvámosla para y:

`(x-2)/(p)=(2-y)/(p)`

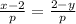
Multiplicamos ambos lados para p y obtenemos:

x-1=2-y

volteamos la ecuación y nos da:

2-y=x-1

pasamos el 2 a restar al otro lado y nos da:

-y=x-1-2

-y=x-3

y dividimos ambos lados de la ecuación dentro de -1

y=-x+3

esta ecuación ya tiene la forma pendiente intercepto:

y=mx+b

donde m es nuestra pendiente:

`m_(1)=-1`

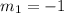
Esta es la pendiente de una de las dos ecuaciones, para que la segunda ecuación sea perpendicular a la primera, su pendiente debe de ser el recíproco negativo de la pendiente de la primera ecuación, entonces la pendiente de la segunda ecuación debe ser:

`m_(2)=-(1)/(m_(1))`

`m_(2)=-(1)/(-1)`

`m_(2)=1`

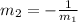
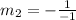
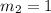
ahora tomamos la segunda ecuación y encontramos su pendiente. Tomemos la ecuación:

`(x-1)/(1-p)=(y-2)/(2)`

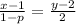
y despejemos y, comenzamos multiplicando ambos lados de la ecuación por 2, así que obtenemos:

`2(x-1)/(1-p)=y-2`

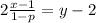
Multiplicamos el 2 por cada término de la fracción, entonces obtenemos:

`(2x-2)/(1-p)=y-2`

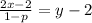
ahora pasamos el 2 a sumar al lado izquierdo y obtenemos:

`(2x-2)/(1-p)+2=y`

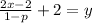
Ahora podemos separar la fracción del lado izquierdo en dos fracciones para obtener:

`(2x)/(1-p)-(2)/(1-p)+2=y`

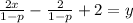
volteamos la ecuación y nos da:

`y=(2x)/(1-p)-(2)/(1-p)+2`

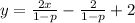
Ahora nuestra ecuación ya tiene la forma y=mx+b

de aquí podemos determinar nuestra pendiente:

`m=(2)/(1-p)`

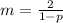
Con la primera ecuación determinamos que esta pendiente debería de ser igual a 1, entonces igualamos esa segunda pendiente a 1 para obtener:

`(2)/(1-p)=1`

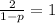
y despejamos p

Pasamos a multiplicat el 1-p al lado derecho de la ecuación para obtener:

2=1-p

volteamos la ecuación:

1-p=2

pasamos el 1 a restar al lado derecho:

-p=2-1

-p=1

y multiplicamos ambos lados de la ecuación por -1 para obtener:

p=-1

Entonces la respuesta es C) solo para el -1