Question

Triangles ABC and ADE are similar, as shown. Which must be true? Check all that apply.

AC=AB
AC/AE=BC/DE
AC/AD=AB/AE
DE=2BC
BC=2DE
AC=2AE
AE=2AC

Answer 1

AC/AE=BC/DE

AC/AD=AB/AE

DE=2BC

AE=2AC

Explanation:

This is what I think.

Answer 2

In similar triangles ABC and ADE, the true statements are: B.
`\( (AC)/(AE) = (BC)/(DE) \)`, D.
`\( DE = 2BC \)`, E.
`\( AE = 2AC \)`.

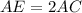The given answer choices involve properties of similar triangles ABC and ADE. Statements B, D, and E are true for similar triangles:

B.
`\( (AC)/(AE) = (BC)/(DE) \)` is true by the definition of similar triangles.

D.
`\( DE = 2BC \)` is true as corresponding sides of similar triangles are in proportion.

E.
`\( BC = 2DE 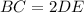\)` is false, as it's the reverse of statement D.

Statement F is incorrect, as AC cannot be equal to
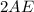`2AE` in similar triangles.

Therefore, B, D, and E must be true for the given pair of similar triangles.