Question

Question 2 (2 points)

Find the indicated limit, if it exists. (2 points)

1) 0
2) 8
3) 3
4) The limit does not exist.

Answer 1

4) The limit does not exist.

General Formulas and Concepts:

Calculus

Limits

• Right-Side Limit:
  `\displaystyle \lim_(x \to c^+) f(x)`
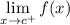
• Left-Side Limit:
  `\displaystyle \lim_(x \to c^-) f(x)`

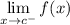
Limit Rule [Variable Direct Substitution]:
`\displaystyle \lim_(x \to c) x = c`

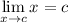
Explanation:

*Note:

For a limit to exist, the right-side and left-side limits must be equal to each other.

Step 1: Define

Identify

`\displaystyle f(x) = \left\{\begin{array}{ccc}5 - x ,\ x < 5\\8 ,\ x = 5\\x + 3 ,\ x > 5\end{array}`

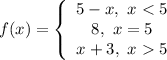
Step 2: Find Left-Side Limit

1. Substitute in function [Left-Side Limit]:
   `\displaystyle \lim_(x \to 5^-) 5 - x`
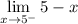
2. Evaluate limit [Limit Rule - Variable Direct Substitution]:
   `\displaystyle \lim_(x \to 5^-) 5 - x = 5- 5 = 0`

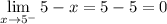
Step 2: Find Left-Side Limit

1. Substitute in function [Right-Side Limit]:
   `\displaystyle \lim_(x \to 5^+) x + 3`
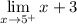
2. Evaluate limit [Limit Rule - Variable Direct Substitution]:
   `\displaystyle \lim_(x \to 5^+) x + 3 = 5 + 3 = 8`

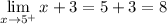
∴ since
`\displaystyle \lim_(x \to c^+) f(x) \\eq \lim_(x \to c^-) f(x)` ,
`\displaystyle \lim_(x \to 5) f(x) = \text{DNE}`

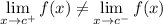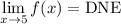
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Limits