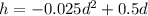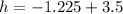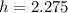Question

Questions 8, 9 and 10 are based on the information below The path of a soccer ball can be defined by the relation h = −0.025d2 +0.5d h = - 0 . 025 d 2 + 0 . 5 d , where h represents the height, in metres, and d represents the horizontal distance, in metres, that the ball travels before it hits the ground

Answer 1

(8) The horizontal distance is 20 meters

(9) Maximum height is 2.5 meters

(c) The height when the horizontal distance is 7 meters is 2.275 meters

Explanation:

Given

`h = -0.025d^2 + 0.5d`

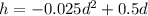
Solving (8): The horizontal distance which the ball lands

When the ball lands, the height is at 0.

So, we have:

`h = -0.025d^2 + 0.5d`

`0 = -0.025d^2 + 0.5d`

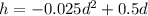
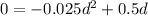
Rewrite as:

`-0.025d^2 + 0.5d = 0`

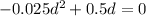
Factorize

`-0.025d(-d+ 20) = 0`

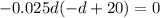
Split

`-0.025d = 0\ or\ -d+ 20 = 0`

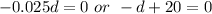
Solve for d

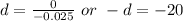
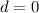`d = (0)/(-0.025)\ or\ -d = -20`

`d = 0` or
`d = 20`

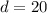
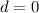`d = 0` ---- This represents the starting point

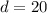`d = 20` ---- This represents the horizontal distance traveled

Solving (9): Maximum height

The maximum of a quadratic equation

`y = ax^2 + bx + c`

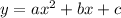
is:

`x = -(b)/(2a)`

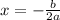
So:
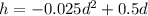`h = -0.025d^2 + 0.5d` means that:

`a = -0.025\ and\ b = 0.5`

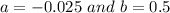
The maximum is:

`d = -(b)/(2a)`

`d = -(0.5)/(2 * -0.025)`

`d = (0.5)/(2 * 0.025)`

`d = (0.5)/(0.05)`

`d = 10`

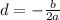
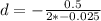
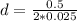
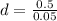
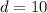
Substitute
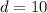`d = 10` in
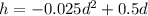`h = -0.025d^2 + 0.5d` to calculate the maximum height

`h = -0.025 * 10^2 + 0.5 * 10`

`h = -2.5 + 5`

`h = 2.5`

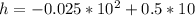
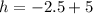
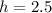
Solving (10): The height when the horizontal distance is 7m

Substitute
`d = 7` in
`h = -0.025d^2 + 0.5d`

`h = -0.025 * 7^2 + 0.5 * 7`

`h = -1.225 + 3.5`

`h = 2.275`