Answer:
This function would have two distinct real roots.
Explanation:
Consider a quadratic function
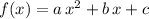 .
.
The determinant of this function would be
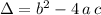 .
.
The (only) two roots of this quadratic function would be:
 , and
, and
 .
.
Because of the square root
 in the two expressions,
in the two expressions,
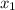 and
and
 would take real values if and only if
would take real values if and only if
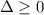 (determinant is nonnegative.) If
(determinant is nonnegative.) If
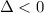 , this quadratic function would not have any real root.
, this quadratic function would not have any real root.
Since the only difference between the two roots
 and
and
 is
is
 , these two roots would repeat one another if
, these two roots would repeat one another if
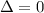 (determinant is zero.)
(determinant is zero.)
Otherwise, if
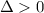 , this quadratic function would have two distinct real roots.
, this quadratic function would have two distinct real roots.