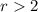Answer:
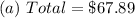
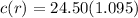 -----
-----
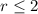
![c(r) = [24.50 + (r - 2)*12.50] * [1.095]](https://img.qammunity.org/2022/formulas/advanced-placement-ap/college/6cl5sajpscdqxiukdkk66og524l8amyktk.png) ----
----
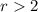
Step-by-step explanation:
Given
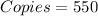
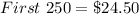

Solving (a): Cost of 550 copies
We have:
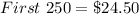
This means that, there are 300 copies left (i.e. 550 - 250)

There are 3 hundreds in 300
So, the cost of the 300 copies is:
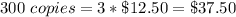
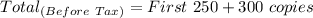
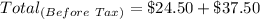
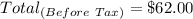
Apply sales tax of 9.5%

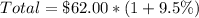
Express percentage as decimal

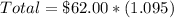

Solving (b): The piece wise function
From the question, we understand that the first 250 cost $24.50
First, we calculate the number of 100s in 250
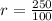
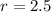
r must be an integer; So, we round down
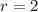
This means that there are 2 whole hundreds in 150.
So, the first function (before tax) is:
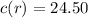 ----
----
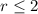
For every other 100 after the first 250
The charge is:
Charge = First 250 + Number of 100s * 12.50
r has a maximum value of 2 for the first 250, this means that the next copies of 100s will have a factor of r - 2
So, the next function (before tax) is:
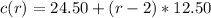 -----
-----
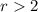
At this point, we have:
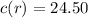 ----
----
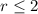
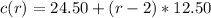 -----
-----
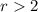
Apply sales tax of 9.5%
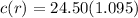 -----
-----
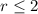
![c(r) = [24.50 + (r - 2)*12.50] * [1.095]](https://img.qammunity.org/2022/formulas/advanced-placement-ap/college/6cl5sajpscdqxiukdkk66og524l8amyktk.png) ----
----