Question

8. Write the equation of the line that is parallel to the line 2x + 5y = 15 and passes through the

point (-10, 1).

Answer 1

Step-1: Convert the line into slope intercept form.

• 2x + 5y = 15
• => 5y = -2x + 15
• => y = -0.4x + 3

Step-2: Use the point slope form formula.

• y - y₁ = m(x - x₁)
• => y - 1 = -0.4{x - (-10)}
• => y - 1 = -0.4{x + 10}
• => y - 1 = -0.4x - 4
• => y = -0.4x - 3

Answer 2

`\sf y = \bold -(2)/(5) x -3`

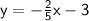
Step-by-step explanation:

part A identification for slope:

`\sf 2x + 5y = 15`

`\sf 5y = -2x + 15`

`\sf y = (-2x + 15)/(5)`

`\sf y = -(2 )/(5) x+3`

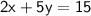
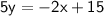
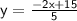
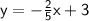
comparing with slope intercept form: y = mx + b

we can find that here the slope is
`\bold -(2)/(5)`

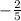
part B, solving the equation:

if the line is parallel, then the slope will be same.

given coordinates: ( - 10, 1 )

using the equation:

y - y₁ = m( x - x₁ )

`\sf y - 1 = \bold -(2)/(5) (x --10)`

`\sf y = \bold -(2)/(5) x -4 + 1`

`\sf y = \bold -(2)/(5) x -3`

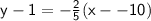
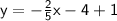
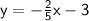
Extra information:

check the image below. this proves that the line is parallel and passes through point (-10, 1). the blue line is question line and red the answer line.