Question

12. From the top A of a building 125m above a street, the angle of elevation of the top B of a second

building on the opposite side is 18'36'and the angle of depression of the base of the second building
from A is 39° 48
(a) Calculate the width of the street​

Answer 1

Answer: 150.02 m

Explanation:

Given

The height of building A is 125 m

the angle of elevation to the top of building B is
`18^(\circ)36'`

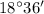
and the angle of depression of the base of Building B is
`39^(\circ)48'`

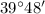
Suppose the width of the street is x

from the figure, we can write

`\Rightarrow \tan (39^(\circ)48')=(125)/(x)\\\\\Rightarrow \tan (39.8^(\circ))=(125)/(x)\\\\\Rightarrow x=(125)/(\tan 39.8^(\circ))\\\\\Rightarrow x=150.02\ m`

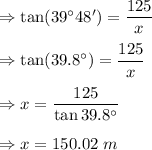
Thus, the width of the street is
`150.02\ m`