Answer:
We have that
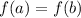 if
if
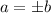 , which does not respect the condition for the existence of an inverse function, which means that
, which does not respect the condition for the existence of an inverse function, which means that
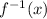 does not exist for this function.
does not exist for this function.
Explanation:
Existence of an inverse function:
An inverse function will exist if: f(a) = f(b) only if a = b.
In this question:
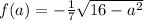
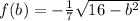
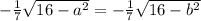
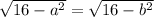
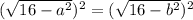
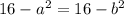
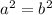
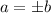
We have that
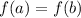 if
if
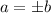 , which does not respect the condition for the existence of an inverse function, which means that
, which does not respect the condition for the existence of an inverse function, which means that
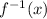 does not exist for this function.
does not exist for this function.