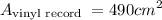Question

No Links!! A vinyl record has a circumference of 78.5 cm. What is its area? Use 3.14 for pi and round to the nearest square cm. please dont just give me 3.14 This is 40% of my grade and i'd really appreciate if someone could help me.

Answer 1

`\displaystyle A _{ \text{vinyl record }} \approx 490 {cm}^(2)`

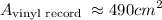
Explanation:

we are given the circumstances of a vinyl record

we want to figure out the area

in order to do so we should figure out redious first

recall that,

`\displaystyle \rm C = 2\pi r`

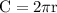
given that, C=78.5

thus substitute:

`\displaystyle \rm 78.5= 2\pi r`

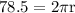
divide both sides by 2π:

`\displaystyle r = (78.5)/(2\pi)`

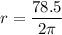
we have figured out r now we'll figure out the area

remember that,

`\displaystyle A _{ \text{circle}} = \pi {r}^(2)`

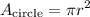
substitute the value of r

`\displaystyle A _{ \text{vinyl record }} = \pi { \bigg((78 .5)/(2\pi) \bigg)}^(2)`

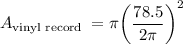
by using calculator we acquire

`\displaystyle A _{ \text{vinyl record }} = 490 {cm}^(2)`