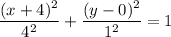Answer:
The equation of the ellipse is;
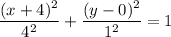
Explanation:
The parameters of the ellipse are;
The location of the center of the ellipse = (-4 0)
The coordinates of the vertex of the ellipse = (-8, 0)
The coordinates of the the co-vertex = (-4, 1)
The general form of the equation of an ellipse is presented as follows;
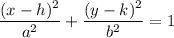
The center of the above equation of an ellipse = (h, k)
The vertex of the above equation are; (h - a, k) and (h + a, k)
The co vertex of the above equation are; (h, k - b) and (h, k + b)
By comparison, we have;
h = -4, k = 0
For the vertex, we have;
When
h - a = -8
∴ -4 - a = -8
-a = -8 + 4 = -4
a = 4
When
h + a = -8
-4 + a = -8
∴ a = -4
a = 4 or -4
We note that a² = 4² = (-4)²
For the covertex, we have;
When
k - b = 1
0 - b = 1
b = -1
When k + b = 1
0 + b = 1
b = 1
∴ b = 1 or -1
b² = 1² = (-1)²
We can therefore write the equation of the ellipse as follows;
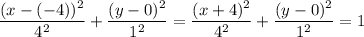
Therefore;