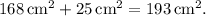Question

3. The net below depicts a triangular prism. What is the total surface area of the prism?

6 cm
5 cm
6 cm
14 cm
com
A. 282 cm
C. 312 cm
B. 210 cm
D. 624 cm

Answer 1

Explanation:

Answer 2

The total surface area of the prism:
`= 193 \, \text{cm}^2\).`

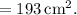
To find the total surface area of a prism, you sum the areas of all the faces. This particular prism is a combination of a rectangular prism and two triangular prisms (due to the trapezoidal faces). The steps to find the total surface area are:

1. Calculate the area of the rectangular faces: The area of a rectangle is found by multiplying its length by its width. For the given prism, you have two rectangular faces with a length of 14 cm and a width of 6 cm.

2. Calculate the area of the triangular faces: The area of a triangle is
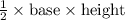`\( (1)/(2) * \text{base} * \text{height} \)`. To find the height of the triangles, you can use trigonometry, knowing the angle and the opposite side. The given angle is 45°, and the opposite side is 5 cm.

3. Calculate the area of the trapezoidal faces: The area of a trapezoid is
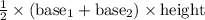`\( (1)/(2) * (\text{base}_1 + \text{base}_2) * \text{height} \)`. You can use the height from the triangles and the known bases (the shorter base is the side of the triangle not against the rectangle, and the longer base is the side of the rectangle).

4. Sum all the areas: Add the areas of the rectangles, triangles, and trapezoids to get the total surface area.

Let's perform the calculations.

The total surface area of the prism is 193 square centimeters. Here's how we arrived at this answer:

1. The area of the rectangular faces:
`\(2 * (14 \, \text{cm} * 6 \, \text{cm}) = 168 \, \text{cm}^2\).`

2. To find the height of the triangles, we used the tangent of the 45-degree angle, which is equal to 1 (since tan(45°) = 1). Therefore, the height of the triangles is equal to the side opposite the angle, which is 5 cm.

3. The area of the triangular faces:
`\(2 * (1)/(2) * 5 \, \text{cm} * 5 \, \text{cm} = 25 \, \text{cm}^2\).`

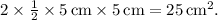
Since the trapezoidal ends of the prism are actually rectangles due to the 45-degree angles (each angle of the triangles forms a right angle with the rectangle), the faces of the trapezoid are already included in the area of the rectangular faces.

4. Summing these areas gives us the total surface area of the prism:
`\(168 \, \text{cm}^2 + 25 \, \text{cm}^2 = 193 \, \text{cm}^2\).`