Answer:
The magnitude of each charge is 1.49*10⁻⁵ C.
Step-by-step explanation:
The electromagnetic force is the interaction that occurs between bodies that have an electric charge.
Coulomb's law is used to calculate the electric force acting between two charges at rest.
This law says that the electrostatic force depends on the distance "r" between the electrons and the charge of both. That is, the magnitude of each of the electric forces with which two point charges interact at rest is directly proportional to the product of the magnitude of both charges and inversely proportional to the square of the distance that separates them. The force is of repulsion if the charges are of the same sign, and of attraction if they are of the opposite sign.
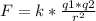
This law is represented as follows:
- F = electric force of attraction or repulsion in Newtons (N).
- k = is the Coulomb constant or electrical constant of proportionality, whose value is: 9*10⁹
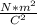
- q = value of electric charges measured in Coulomb (C).
- r = distance that separates the charges and that is measured in meters (m).
In this case:
- F= 8 N
- q1=q2= q= ?
- r= 0.50 m
Replacing:
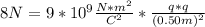
Solving:
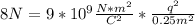
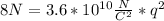
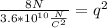

1.49*10⁻⁵ C=q
The magnitude of each charge is 1.49*10⁻⁵ C.