Question

A report about how American college students manage their finances includes data from a survey of college students. Each person in a representative sample of 793 college students was asked if they had one or more credit cards and if so, whether they paid their balance in full each month. There were 500 who paid in full each month. For this sample of 500 students, the sample mean credit card balance was reported to be $825. The sample standard deviation of the credit card balances for these 500 students was not reported, but for purposes of this exercise, suppose that it was $195. Is there convincing evidence that college students who pay their credit card balance in full each month have a mean balance that is lower than $907, the value reported for all college students with credit cards?

Required:
a. Carry out a hypothesis test using& significance level of 0.01.
b. State the appropriate null and alternative hypotheses.

Answer 1

Following are the responses to the given question:

Explanation:

Test statistic:

`t=((825-905))/((205)/(√((500))))`

`=((-80))/((205)/(22.36))\\\\=((-80))/(9.16)\\\\=-8.73`

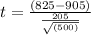
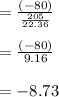
Let the p-value=0

We reject H0 because of the p-value <0.01. We have evidence that college kids who pay their credit card bills in full per month have a mean balance of less than $905.