Question

A study by Consumer Reports showed that 64% of supermarket shoppers believe supermarket brands to be as good as national name brands. the manager of the Publix in Clemson believes 64% is too low for his own store, to investigate whether this result applies to its own store, SC asked a random sample of 100 shoppers whether they believed that supermarket brands were as good as the national brands, 52 believe the supermarket brands were as good as the national brands.

Required:
At the 10% significance level test the managers claim.

Answer 1

The calculated value |Z| = |-2.5| >2.326 at 0.05 level of significance

The alternative hypothesis is accepted at a 0.05 level of significance

The manager of Publix in Clemson believes 64% is too high for his own store

Explanation:

Step:-1

Given that the consumer Reports showed that 64% of supermarket shoppers.

Given that the population proportion

P = 0.64

Given that random sample size 'n' = 100

Given that 52 believe the supermarket brands were as good as the national brands.

sample proportion

`p^(-) = (x)/(n) = (52)/(100) = 0.52`

Step:-2

Null hypothesis: The manager of the Publix in Clemson believes 64% is too low for his own store

μ < 0.64

Alternative Hypothesis:H₁:μ > 0.64

Test statistic

`Z = \frac{p-P}{\sqrt{(PQ)/(n) } }`

`Z = \frac{0.52-0.64}{\sqrt{(0.64 X 0.36)/(100) } }`

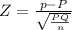
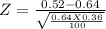
Z = -2.5

Level of significance = 0.05

Z₀.₀₅ = 2.326

The calculated value |Z| = |-2.5| >2.326 at 0.05 level of significance

Final answer:-

The null hypothesis is rejected at a 0.05 level of significance

The alternative hypothesis is accepted at a 0.05 level of significance