Question

Nitrogen effuses through a pinhole 1.7 times as fast as another gaseous element under the same conditions. Estimate the other element’s molar mass and determine its probable identity.

Answer 1

80.92, Krypton

Step-by-step explanation:

What is effusion?

• It is a process where gas escapes through a pinhole (a very small hole) into a region of low pressure or vacuum

Graham's law of effusion of gas

• states that at a given constant temperature and pressure, the rate of effusion of gases is inversely proportional to the square root of their molar masses

`\boxed{ (Rate_1)/(Rate_2) = \sqrt{ (M_2)/(M_1) } }`

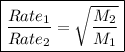
Calculations

Nitrogen exist as N₂ at room temperature, thus its molar mass is 2(14)= 28.

Let the rate and molar mass of unknown gas be Rate₂ and M₂ respectively.

Since N₂ effuses 1.7 times as fast as the unknown gas,

Rate₁= 1.7(Rate₂)

`(Rate_1)/(Rate_2) = 1.7`

`1. 7 = \sqrt{ (M_2)/(28) }`

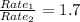
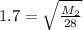
Square both sides:

`2.89 = (M_2)/(28)`

Multiply both sides by 28:

2.89(28)= M₂

M₂= 80.92

Identity of gas

The molar mass of 80.92 lies between Bromine and Krypton. However since Bromine exist as Br₂, the value of it's molar mass would be 159.8 instead. Hence, Bromine is eliminated.

If the gas is a diatomic element, the atomic weight is 80.92 ÷2= 40.46. Thus, we are now considering if Argon could be its identity. However, Argon is a noble gas and will not exist as a diatomic element. Argon is therefore eliminated too.

Thus based on the above reasoning, its probable identity is Krypton.