Answer:
The 99% of a confidence interval for the average maximum HP for the experimental engine.
(536.46, 603.54)
Explanation:
Step:-1
Given that the mean of the Population = 540HP
Given that the size of the sample 'n' = 9
Given that the mean of the sample = 570HP
Given that the sample standard deviation = 30HP
Step(ii):-
Degrees of freedom = n-1 =9-1 =8
t₀.₀₀₅ = 3.3554
The 99% of a confidence interval for the average maximum HP for the experimental engine.
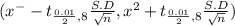
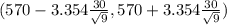
(570 - 33.54 , 570+33.54)
(536.46 , 603.54)
Final answer :-
The 99% of a confidence interval for the average maximum HP for the experimental engine.
(536.46, 603.54)