Question

Jay places $3200 in an investment account earning 4.1% interest compounded weekly. How much money would he have in the account after 5 years, if he made no deposits or withdrawals during that time?

Answer 1

A = $3,926.71

Explanation:

Given: Principal (P) = $3200, Annual Rate (R) = 4.1%, Time = 5 years

To find: How much money would he have in the account after 5 years, if he made no deposits or withdrawals during that time?

Formula:
`A = P(1 + r/n)^nt`

Solution: Compound interest is one of the most important concepts to understand when managing your finances. It can help you earn a higher return on your savings and investments, but it can also work against you when you're paying interest on a loan

First, convert R as a percent to r as a decimal

r = R/100

r = 4.1/100

r = 0.041 rate per year,

Then solve the equation for A

A = P(1 + r/n)
`^(nt)`

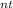
A = 3,200.00(1 + 0.041/12)
`^((12)(5))`

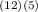
A = 3,200.00(1 + 0.003416667)
`^((60))`

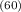
A = $3,926.71

Hence, Jay would have $3,926.71 after 5 years is if he made no deposits or withdrawals during that time.