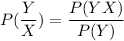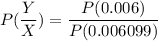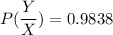Question

A student S is suspected of cheating on exam, due to evidence E of cheating being present. Suppose that in the case of a cheating student, evidence E is present with 60% percent probability, and in the case of a student that does not cheat, evidence E is present with a 0.01 percent probability. Suppose also that the proportion of students that cheat is 1 percent. Show all the steps including identification of what formulas/properties you used. Points will be deducted from answers if only the final answer is provided.

Required:
a. Determine the events, given probabilities and inferred probabilities.
b. Determine the probability that the evidence is present.
c. Determine the probability that S cheated given the evidence is present.

Answer 1

Explanation:

Suppose we think of an alphabet X to be the Event of the evidence.

Also, if Y be the Event of cheating; &

Y' be the Event of not involved in cheating

From the given information:

`P((X)/(Y)) = 60\% = 0.6`

`P((X)/(Y')) = 0.01\% = 0.0001`

`P(Y) = 0.01`

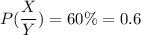
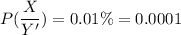
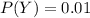
Thus,
`P(Y') \ will\ be = 1 - P(Y)`

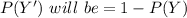
P(Y') = 1 - 0.01

P(Y') = 0.99

The probability of cheating & the evidence is present is = P(YX)

`P(YX) = P((X)/(Y)) \ P(Y)`

`P(YX) =0.6 * 0.01`

`P(YX) =0.006`

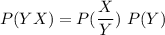
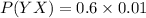
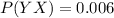
The probabilities of not involved in cheating & the evidence are present is:

`P(Y'X) = P(Y') * P((X)/(Y'))`

`P(Y'X) = 0.99 * 0.0001 \\ \\ P(Y'X) = 0.000099`

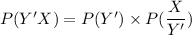
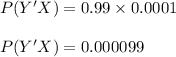
(b)

The required probability that the evidence is present is:

P(YX or Y'X) = 0.006 + 0.000099

P(YX or Y'X) = 0.006099

(c)

The required probability that (S) cheat provided the evidence being present is:

Using Bayes Theorem

`P((Y)/(X)) = (P(YX))/(P(Y))`

`P((Y)/(X)) = (P(0.006))/(P(0.006099))`

`P((Y)/(X)) = 0.9838`