Answer:
A) 1.3013476 × 10²⁸ N·m
b) 2.8618128 × 10²⁹ J
c) 4.73183333 × 10²³ W
Step-by-step explanation:
The mass of the Earth, M = 5.972 × 10²⁴ kg
The radius of the Earth, R = 6,371 km
The angular speed of the Earth, ω = 2·π/(24 hr) = 7.27220522 × 10⁻⁵ rad/s
The shape of the Earth ≈ Spherical
The moment of inertia of a sphere, I = (2/5)·M·R²
The angular acceleration of the Earth in 7 days from rest its present angular speed, ω, is given as follows;
α = 7.27220522 × 10⁻⁵ rad/s/((7 × 24 × 60 × 60) s) = 1.2024149 × 10⁻¹⁰ rad/s²
Torque, τ = I × α
∴ τ = (2/5) × 5.972 × 10²⁴ × 6,731,000² × 1.2024149 × 10⁻¹⁰ = 1.3013476 × 10²⁸
The torque required, τ = 1.3013476 × 10²⁸ N·m
b) The energy required,
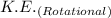 = 1/2 × I × ω²
= 1/2 × I × ω²
∴
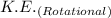 = (1/2) × (2/5) × 5.972 × 10²⁴ × 6,731,000² × (7.27220522 × 10⁻⁵ rad/s)²
= (1/2) × (2/5) × 5.972 × 10²⁴ × 6,731,000² × (7.27220522 × 10⁻⁵ rad/s)²
The energy required,
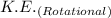 = 2.8618128 × 10²⁹ J
= 2.8618128 × 10²⁹ J
c) Power = Energy/Time
Therefore, the average power required, P =
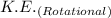 /Time
/Time
∴ P = 2.8618128 × 10²⁹ J/(7 × 24 × 60 × 60) s) = 4.73183333 × 10²³ Watts
The average power required, P = 4.73183333 × 10²³ Watts.