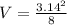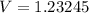Answer:
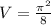
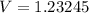
Explanation:
Given
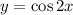
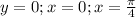
Required
Determine the volume of the solid generated
Using the disk method approach, we have:
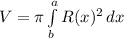
Where
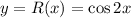
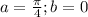
So:
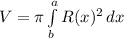
Where
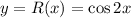
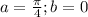
So:
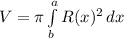
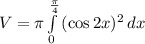
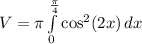
Apply the following half angle trigonometry identity;
![\cos^2(x) = (1)/(2)[1 + \cos(2x)]](https://img.qammunity.org/2022/formulas/mathematics/college/70kjjo3t19avyby6d3cvw0x6pru1wfakt0.png)
So, we have:
![\cos^2(2x) = (1)/(2)[1 + \cos(2*2x)]](https://img.qammunity.org/2022/formulas/mathematics/college/1b4knzzyqsi26m5h2sj5jl1nu4ebffi4tq.png)
![\cos^2(2x) = (1)/(2)[1 + \cos(4x)]](https://img.qammunity.org/2022/formulas/mathematics/college/qcdvyruu05hwm2b5c8kf24m8wnqsmfht3w.png)
Open bracket
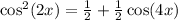
So, we have:
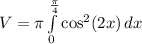
![V = \pi \int\limits^{(\pi)/(4)}_0 {[(1)/(2) + (1)/(2)\cos(4x)]} \, dx](https://img.qammunity.org/2022/formulas/mathematics/college/60jan7yl73syep0hh896w1i6awfrsgzcgl.png)
Integrate
![V = \pi [(x)/(2) + (1)/(8)\sin(4x)]\limits^{(\pi)/(4)}_0](https://img.qammunity.org/2022/formulas/mathematics/college/b049t2da4841hur3xt8galu8n70mwc66sj.png)
Expand
![V = \pi ([((\pi)/(4))/(2) + (1)/(8)\sin(4*(\pi)/(4))] - [(0)/(2) + (1)/(8)\sin(4*0)])](https://img.qammunity.org/2022/formulas/mathematics/college/5w6mxadye7nz2i2e3hiybpzy8ie9uz9f14.png)
![V = \pi ([((\pi)/(4))/(2) + (1)/(8)\sin(4*(\pi)/(4))] - [0 + 0])](https://img.qammunity.org/2022/formulas/mathematics/college/68dmmcee4qkz979undq6mu4ytt4h8ml24n.png)
![V = \pi ([((\pi)/(4))/(2) + (1)/(8)\sin(4*(\pi)/(4))])](https://img.qammunity.org/2022/formulas/mathematics/college/mrobalrfmehq5l72gajidg4j0kk8c34127.png)
![V = \pi ([{(\pi)/(8) + (1)/(8)\sin(\pi)])](https://img.qammunity.org/2022/formulas/mathematics/college/4pfd22a513txi99qdfr8nbnkehgqga00a4.png)
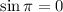
So:
![V = \pi ([{(\pi)/(8) + (1)/(8)*0])](https://img.qammunity.org/2022/formulas/mathematics/college/nm8a2a5asqx5pv8vs2rz77ed9dyo4kwpge.png)
![V = \pi *[{(\pi)/(8)]](https://img.qammunity.org/2022/formulas/mathematics/college/5p0q2sqyb5fhaptsjcnzpi9ptm92awnnyg.png)
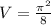
or