Answer:
The coordinates of B' and C' are
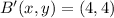 and
and
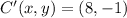 .
.
Explanation:
Vectorially speaking, the translation of a point is represented by the following operation:
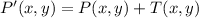 (1)
(1)
Where:
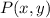 - Original point.
- Original point.
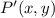 - Translated point.
- Translated point.
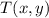 - Translation vector.
- Translation vector.
First, we need to calculate the translation vector after knowing that
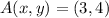 and
and
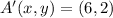 . That is:
. That is:
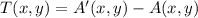
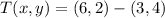
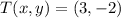
Finally, we determine the coordinates of points B' and C':
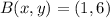 ,
,
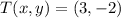
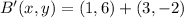
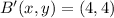
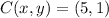 ,
,
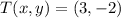
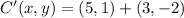
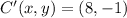
The coordinates of B' and C' are
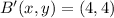 and
and
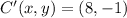 .
.