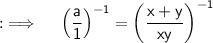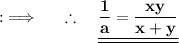We are given that a =(1/x) + (1/y) , and need to find the value of (1/a) , as a is the sum of two fractions so we can't reciprocal both sides directly without finding their sum and converting them into a single fraction . So , let's start by simplifying a first
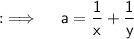
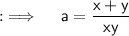
Now , we knows an indentity ;
Now , raising to the power -1 on both sides :