Question

A manufacturer of potato chips would like to know whether its bag filling machine works correctly at the 444 gram setting. It is believed that the machine is underfilling the bags. A 9 bag sample had a mean of 441 grams with a standard deviation of 25. A level of significance of 0.025 will be used. Assume the population distribution is approximately normal.

Required:
Is there sufficient evidence to support the claim that the bags are underfilled?

Answer 1

The pvalue of the test is 0.3641 > 0.025, which means that there is not sufficient evidence to support the claim that the bags are underfilled.

Explanation:

A manufacturer of potato chips would like to know whether its bag filling machine works correctly at the 444 gram setting. Test if they are underfilled:

At the null hypothesis, we test if the mean is the correct mean of 444, that is:

`H_0: \mu = 444`

At the alternate hypothesis, we test if it is underfilled, that is, the mean is less than 444.

`H_a: \mu < 444`

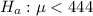
The test statistic is:

`t = (X - \mu)/((s)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis, s is the standard deviation and n is the size of the sample.

444 is tested at the null hypothesis:

This means that
`\mu = 444`

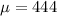
A 9 bag sample had a mean of 441 grams with a standard deviation of 25.

This means that
`n = 9, X = 441, s = 25`

Value of the test statistic:

`t = (X - \mu)/((s)/(√(n)))`

`t = (441 - 444)/((25)/(√(9)))`

`t = -0.36`

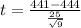
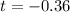
Pvalue of the test and decision:

The pvalue of the test is the probability of finding a mean of 441 or less, which is the pvalue of t = -0.36, with 9 - 1 = 8 degrees of freedom on a one-tailed test.

Using a calculator, the pvalue is 0.3641.

The pvalue of the test is 0.3641 > 0.025, which means that there is not sufficient evidence to support the claim that the bags are underfilled.