Question

For problems 1, 2, and 3, use the function g(x) = sin(6x) .

1. Find the amplitude of the function. State the range of the function.

2. Find the period of the function. Find the key points of the function [intercept(s), maximum(s), and minimum(s)] for 1 period. Show all work.

3. Sketch the graph of g (one period), alongside the graph of f(x) = sinx on the interval [0,2/pi]. Label the axes.

For problems 4, 5, and 6, use the function g(x)=cos((x)/(4)).

4. Find the amplitude of the function. State the range of the function.

5. Find the period of the function. Find the key points of the function [intercept(s), maximum(s), and minimum(s)] for 1 period. Show all work.

6. Sketch the graph of g, alongside the graph of f(x) = cosx on the interval [0,2/pi] . Label the axes.

Answer 1

Explanation:

1. Amplitude = 1. g(x) = 1 sin(6x). The coefficient 1 is the amplitude. The range of the function is
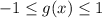`-1 \le g(x) \le 1` or, in interval notation, [-1, 1]

2. The period is
`(2\pi)/(6)=(\pi)/(3)`.

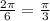x-intercepts (at the beginning, middle, and end of the period)
`0,\,(\pi)/(6),\,(\pi)/(3)`

Maximum (1/4 of way through period)
`\left((\pi)/(12),\,1 \right)`

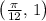
Minimum (3/4 of way through period)
`\left( (\pi)/(4), \, -1 \right)`