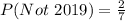Answer:
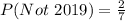
Explanation:
Given
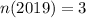
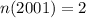

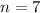 --- total
--- total
Required

When two quarters not minted in 2019 are selected, the sample space is:
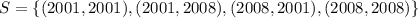
So, the probability is:
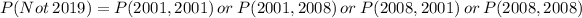
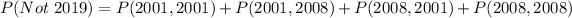
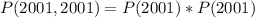
Since it is a selection without replacement, we have:

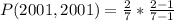
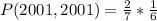
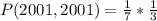
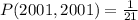
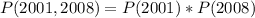
Since it is a selection without replacement, we have:
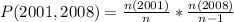
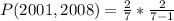
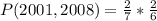
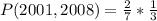
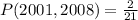
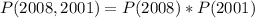
Since it is a selection without replacement, we have:
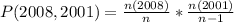
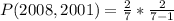
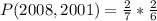


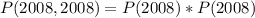
Since it is a selection without replacement, we have:
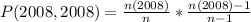

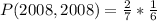
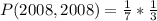
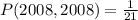
So:
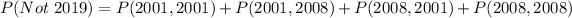
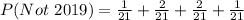
Take LCM
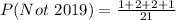
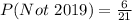
Simplify