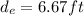Question

To balance a seesaw, the distance a person is from the fulcrum is inversely proportional to his or her weight . Roger , who weighs 120 pounds is sitting 6 feet from the fulcrum . Ellen weighs 108 pounds . How far from the fulcrum must she sit to balance the seesaw ? Round to the nearest hundredth of a foot .

Answer 1

`d_e =6.67ft`

Explanation:

From the question we are told that:

Weight of Roger
`W_r=120\ pounds`

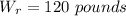
Distance of Roger from fulcrum
`d_r=6 ft`

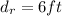
Weight of Ellen
`W_e=120\ pounds`

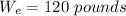
Generally the equation for distance-weight relationship is mathematically given by

`d\alpha (1)/(W)`

`(d_1)/(d_2) =(W_2)/(W_1)`

`(d_r)/(d_e) =(W_e)/(W_r)`

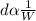
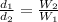
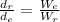
Therefore

`(d_e)/(d_r) =(W_r)/(W_e)`

`d_e =(W_r*d_r)/(W_e)`

`d_e =(6*120)/(108)`

`d_e =6.67ft`

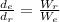
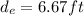
Therefore the distance from the fulcrum she must sit to balance the seesaw is given as

`d_e =6.67ft`