Question

The American Water Works Association reports that the per capita water use in a single-family home is 69 gallons per day. Legacy Ranch is a relatively new housing development. The builders installed more efficient water fixtures, such as low-flush toilets, and subsequently conducted a survey of the residences. Thirty-six owners responded, and the sample mean water use per day was 64 gallons with a standard deviation of 8.8 gallons per day.

Required:
At the 0.10 level of significance, is that enough evidence to conclude that residents of Legacy Ranch use less water on average?

Answer 1

The pvalue of the test is 0.0083 < 0.1, which means that there is enough evidence to conclude that residents of Legacy Ranch use less water on average

Explanation:

The American Water Works Association reports that the per capita water use in a single-family home is 69 gallons per day. Test that the residents use less water.

At the null hypothesis, we test that the mean is 69, that is:

`H_0: \mu = 69`

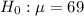
At the alternate hypothesis, we test that the mean is less than 69, that is:

`H_a: \mu < 69`

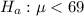
The test statistic is:

As we have the standard deviation for the sample, we use the t-statistic.

`t = (X - \mu)/((s)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis, s is the standard deviation and n is the size of the sample.

69 is tested at the null hypothesis:

This means that
`\mu = 69`

Thirty-six owners responded, and the sample mean water use per day was 64 gallons with a standard deviation of 8.8 gallons per day.

This means that
`n = 36, X = 64, s = 8.8`

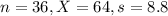
Value of the test statistic:

`t = (X - \mu)/((s)/(√(n)))`

`t = (64 - 69)/((8.8)/(√(36)))`

`t = -3.41`

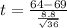
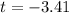
Pvalue of the test and decision:

The pvalue of the test is the probability of finding a mean less than 64, which is the pvalue of t = -3.41, found on the t-table with 36 - 1 = 35 degrees of freedom on a one-tailed test.

With calculator help, the pvalue is 0.0083.

The pvalue of the test is 0.0083 < 0.1, which means that there is enough evidence to conclude that residents of Legacy Ranch use less water on average