Question

(25points) Which of the following is the ratio of the area of the shaded region to the total area of the square

a)1/2
b)1/3
c)3/8
d)3/4

Answer 1

C

Explanation:

We want to find ratio of the area of the shaded region to the total area of the square.

First, we can find the total area of the square. Since QR = 7, each side of the square measures 7. Therefore, its area is:

`A=(7)^2=49\text{ units}^2`

Instead of finding the shaded area, we can find the areas that are not shaded. Subtracting that into the total area will then give us the shaded area.

QRP is a triangle. Since PQRS is a square, QR = 7 = RS = SP = PQ.

So, the area of ΔQRP is:

`\displaystyle A_(\Delta QRP)=(1)/(2)(7)(7)=24.5`

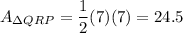
UTS is also a triangle. We are given that RU = US and PT = TS. So, Points U and T bisect RS and SP, respectively. Since RS = SP = 7, RU = US = PT = TS = 3.5. So, the area of ΔUTS is:

`\displaystyle A_(\Delta UTS)=(1)/(2)(3.5)(3.5)=6.125`

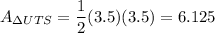
Therefore, the total area of the white region is:

`A_{\text{white}}=6.125+24.5=30.625`

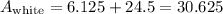
Thus, the shaded region is:

`A_{\text{shaded}}=49-30.625=18.375`

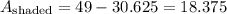
Then the ratio of the shaded region to the total area of the square will be:

`\displaystyle R_{\text{shaded:total}}=(18.375)/(49)=(3)/(8)`

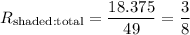
Our answer is C.