Question

In marketing, response modeling is a method for identifying customers most likely to respond to an advertisement. Suppose that in past campaigns 23.8% of customers identified as likely respondents did not respond to a nationwide direct marketing campaign. After making improvements to their model, a team of marketing analysts hoped that the proportion of customers identified as likely respondents who did not respond to a new campaign would decrease. The analysts selected a random sample of 1500 customers and found that 315 did not respond to the marketing campaign.

The marketing analysts want to use a one-sample z-test to see if the proportion of customers who did not respond to the advertising campaign, p, has decreased since they updated their model. They decide to use a significance level of α= 0.01.

Required:
a. Determine the value of the z-statistic. Give your answer precise to at least two decimal places.
b. Determine the p-value for this test. Give your answer precise to at least three decimal places.

Answer 1

a) The value of the z-statistic is z = -2.55.

b) The p-value for this test is 0.0054.

Explanation:

Suppose that in past campaigns 23.8% of customers identified as likely respondents did not respond to a nationwide direct marketing campaign. Test if this proportion has decreased:

This means that at the null hypothesis we test that if the proportion is still 0.238, that is:

`H_0: p =0.238`

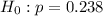
And at the alternate hypothesis we test if the proportion has decreased, that is:

`H_a: p < 0.238`

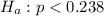
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

0.238 is tested at the null hypothesis:

This means that
`\mu = 0.238, \sigma = √(0.238*0.762)`

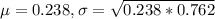
The analysts selected a random sample of 1500 customers and found that 315 did not respond to the marketing campaign.

This means that
`n = 1500, X = (315)/(1500) = 0.21`

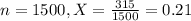
a. Determine the value of the z-statistic. Give your answer precise to at least two decimal places.

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (0.21 - 0.238)/((√(0.238*0.762))/(√(1500)))`

`z = -2.55`

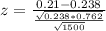
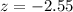
The value of the z-statistic is z = -2.55.

b. Determine the p-value for this test. Give your answer precise to at least three decimal places.

The p-value of the test is the probability of finding a proportion below 0.21, which is the p-value of z = -2.55.

Looking at the z-table, z = -2.55 has a p-value of 0.0054

The p-value for this test is 0.0054.