Answer:
<ACB =
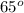 and <BAC =
and <BAC =
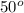
Explanation:
The given triangle is an isosceles triangle. Thus its two sides are equal and base angles are equal.
So that;
<ACB = <ABC
<ACB =
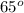 (property of an isosceles triangle)
(property of an isosceles triangle)
Then,
<ABC + <ACB + <BAC =
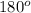
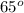 +
+
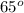 + <BAC =
+ <BAC =
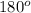
130 + <BAC =
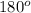
<BAC =
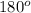 -
-
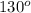
=
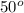
<BAC =
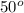
Thus, <ACB =
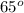 and <BAC =
and <BAC =
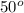 .
.