Question

An aircraft factory manufactures airplane engines. The unit cost C (the cost in dollars to make each airplane engine) depends on the number of engines made. If x engines are made, then the unit cost is given by the function C(x)=x2-180x+20,482. How many engines must be made to minimize the unit cost? Do not round your answer.​

Answer 1

90 engines must be made to minimize the unit cost.

Explanation:

Vertex of a quadratic function:

Suppose we have a quadratic function in the following format:

`f(x) = ax^(2) + bx + c`

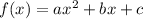
It's vertex is the point
`(x_(v), y_(v))`

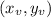
In which

`x_(v) = -(b)/(2a)`

`y_(v) = -(\Delta)/(4a)`

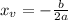
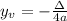
Where

`\Delta = b^2-4ac`

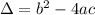
If a>0, the minimum value of the function will happen for
`x = x_v`

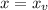
C(x)=x²-180x+20,482

This means that
`a = 1, b = -180, c = 20482`

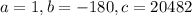
How many engines must be made to minimize the unit cost?

x value of the vertex. So

`x_(v) = -(b)/(2a) = -(-180)/(2(1)) = 90`

90 engines must be made to minimize the unit cost.