Answer:
The tank must remain intact for 1183 years.
Explanation:
Exponential equation for decay:
The amount of a substance after t years is given by:
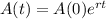
In which A(0) is the initial amount and r is the decay rate.
A storage tank contains a liquid radioactive element with a half-life of 96 years.
This means that
 , and we use this to find r.
, and we use this to find r.
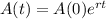
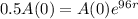

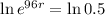
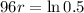


So
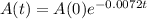
It will be relatively safe for the contents to leak from the tank when 0.02% of the radioactive element remains. How long must the tank remain intact for this storage procedure to be safe?
This is t for which
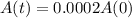 . So
. So
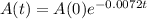
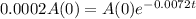
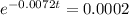
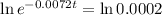
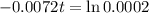
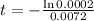
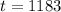
The tank must remain intact for 1183 years.