Answer:
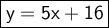
Explanation:
Here it is given that a line c has a equation of ,

And there is another line d which is parallel to line c and passes through the point (-4,-4) . And we need to find out the equation of the line .
Firstly we know that the slope of two parallel lines is same . So on comparing the given line to the slope intercept form of the line which is y = mx + c , we have ;
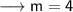
Therefore the slope of the parallel line will be ,
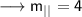
On using the point slope form of the line , we have ;
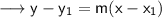
Substitute the values ,
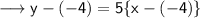
Simplify ,
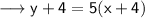
Open the brackets ,
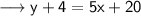
Subtract 4/on both sides ,
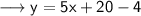
Simplify ,
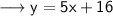
Hence the equation of the line is y = 5x + 16