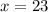Answer:
The smaller number is 23
Explanation:
Given
Let the odd numbers be x and y [x, being the smallest]
Such that
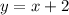
and
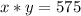
Required
Find x
Substitute
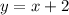 in
in
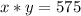
![x * [x + 2] = 575](https://img.qammunity.org/2022/formulas/mathematics/college/svauepr1mgqwp6xpnjtvrvqosb8k2xoafb.png)
Open bracket
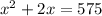
Equate to 0
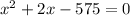
Expand
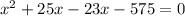
Factorize
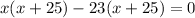
Factor out x + 25
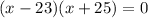
Solve
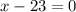 or
or
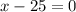
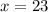 or
or
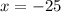
But x can't be negative.
So: