Answer:
The p-value is 0.1867.
Explanation:
Employees at a construction and mining company claim that the mean salary of the company's mechanical engineers is less than that of the one of its competitors, which is $68,000.
At the null hypothesis we test that the salary is the same of the competitor, that is:
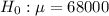
At the alternate hypothesis, we test that it is more than 68000. So
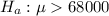
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
68000 is tested at the null hypothesis:
This means that
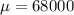
A random sample of 20 of the company's mechanical engineers has a mean salary of $66,900. Assume the population standard deviation is $5500.
This means that
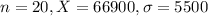
Value of the test statistic:

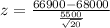
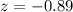
P-value:
The pvalue is the probability of finding a sample mean below 66900, which is the pvalue of z = -0.89.
Looking at the z-table, z = -0.89 has a pvalue of 0.1867.
The p-value is 0.1867.