Answer:
k = 652 lb/ft
Step-by-step explanation:
Given :
Weight of the collar = 1.6 lb
The upstretched length of the spring = 6 in
Speed = 16 ft/s
PA = 8 + 10
= 18 inch
Let the initial elongation be
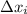
∴
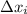 = 18 - 6
= 18 - 6
= 12 inch = 1 foot
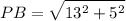
= 13.925 inch
Final elongation in the spring
 inch = 0.66 feet
inch = 0.66 feet
Applying the conservation of the mechanical energy between A and B is
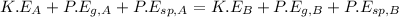
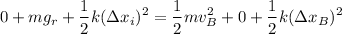
![$(1)/(2)k[(1)^2-(0.66)^2]=(1.6)/(2)* (16)^2-1.6 * 32 * (5)/(12)$](https://img.qammunity.org/2022/formulas/physics/college/zenkwmja92313jenmt0v5bmphn11p0zrfy.png)
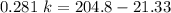
k = 652 lb/ft