Question

A sample of radon gas has a volume of 0.650 L at a temperature of -55.0 C. What volume will the gas occupy at 40.0 C, assuming constant pressure?

Answer 1

0.933 L

Step-by-step explanation:

Since the pressure is the same, we use the equation
`(V_(1))/(T_(1) ) = (V_(2) )/(T_(2) )`

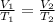
V = Volume

T = Temperature

Since we are given the temperature in Celsius, we need to convert it to Kelvin by adding 273:

-55.0 + 273 = 218

40.0 + 273 = 313

`(0.650)/(218) = (x)/(313)`

`0.933 = x`

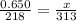
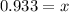
The gas will occupy a volume of 0.933 L.

(Side note - If the temperature increases, the gas will want to expand, leading to a higher volume.)