Answer:
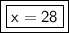
Explanation:
This is a right triangle. The small square in the corner represents a 90 degree angle. We can use trigonometry. The three major ratios are:
- sin(θ)=opposite/hypotenuse
- cos(θ)=adjacent/hypotenuse
- tan(θ)= opposite/adjacent
The angle, or θ, is 60 degrees. The side measuring 14 is adjacent to this angle. x is the hypotenuse because it is opposite the right angle. Since we have the adjacent side and the hypotenuse, we use cosine.
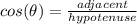

Since we are solving x, we must isolate the variable. First, cross multiply.
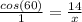
Multiply the first numerator (cos60) by the second denominator (x).
Then, multiply the first denominator (1) by the second numerator (14)
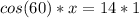
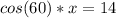
The cosine of 60 is equal to 1/2,
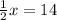
x is being multiplied by 1/2. The inverse of multiplication is division. Divide both sides of the equation by 1/2. Since this is a fraction, you can also multiply by the reciprocal: 2.

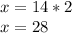
The hypotenuse, x, is equal to 28.