Question

Harry bought a broken motor scooter, fixed it, and sold the scooter for $150. That was $25 less than 2 times the amount he paid for it. Which equation can be used to find, p, the amount of money Harry originally paid for the scooter?

Answer 1

P = 150 ÷ 2 - 25 = p

Explanation:

The equation of a line is typically written as y=mx+b where m is the slope and b is the y-intercept. If you know two points that a line passes through, this page will show you how to find the equation of the line.

Given: Harry bought a broken motor scooter, fixed it, and sold the scooter for $150. $25 less than 2 times the amount he paid for it.

To find: Which equation can be used to find, p, the amount of money Harry originally paid for the scooter?

Solution: It says; "That was $25 less than 2 times the amount he paid for it"

With that said, find the amount that is 2 times more than 150. To find that, the opposite of times is division, so divide 150 by 2

`150` ÷
`2 =`
`75`

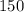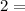
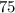
Now that has been found, the next thing to find is $25 less, less means subtract. To calculate the amount Harry originally paid for the scooter, subtract 25 from 75

`75 - 25 = 50`

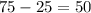
Therefore, the amount of money Harry originally paid for the scooter is $50

Hence, the equation can now be found as; P = 150 ÷ 2 - 25 = p

Answer 2

p/2 - 25 = 150

Explanation:

I'll try my best.

$150 would be the initial value, so we would use that for the base.

$25 less means subtract 25 dollars in this context.

2 times means multiply by 2.

"$150 was $25 less than 2 times the amount he paid for it (
`p`)."

`(p)/(2) -25 = 150`

If you were to solve this:

`(p)/(2) -25 = 150`

`(p)/(2) =175`

`p=350`

The answer I get from the equation would be $350.

If you input 350 into it:

`((350))/(2) -25`

`175 -25`

`150`