Question

A 4.00-kg block hangs by a light string that passes over a massless, frictionless pulley and is connected to a 6.00-kg block that rests on a frictionless shelf. The 6.00-kg block is pushed against a spring to which it is not attached. The spring has a spring constant of 180 N/m, and it is compressed by 30.0 cm. Find the speed of the block after the spring is released and the 4.00-kg block has fallen a distance of 40.0 cm.

Answer 1

v = 2.82 m/s

Step-by-step explanation:

For this exercise we can use the conservation of energy relations.

We place our reference system at the point where block 1 of m₁ = 4 kg

starting point. With the spring compressed

Em₀ = K_e + U₂ = ½ k x² + m₂ g y₂

final point. When block 1 has descended y = - 0.400 m

Em_f = K₂ + U₂ + U₁ = ½ m₂ v² + m₂ g y₂ + m₁ g y

as there is no friction, the energy is conserved

Em₀ = Em_f

½ k x² + m₂ g y₂ = ½ m₂ v² + m₂ g y₂ + m₁ g y

½ k x² - m₁ g y = ½ m₂ v²

v² =
`(k)/(m_2) x^2 - 2 (m_1)/(m_2) \ g y`

let's calculate

v² =
`(180)/(6.00) \ 0.300^2 - 2 \ (4.00)/(6.00) \ 9.8 \ (- 0.400)`

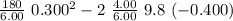
v² = 2.7 + 5.23

v = √7.927

v = 2,815 m / s

using of significant figures

v = 2.82 m/s